Nonlinear separation of a show-through mixtures using a physical model trained with ICA

(Abstract, Bi-affine separability, Data)

Acquired Separated

page images page images

Reference:

M. S. C. Almeida and L. B. Almeida, “Nonlinear saparation of a show-through mixing model using a physical model trained with ICA”, Signal Processing, Vol 92, issue 4, pp. 872-884, April, 2012. (Online)

Abstract:

Often, when we scan a document, the image from the back page shows through, due to partial transparency of the paper, giving rise to a mixture of two images. We address the problem of separating these images through the use of a physical model of the mixture process. The model is nonlinear but invertible, and we use the inverse model to perform the separation. The model is trained through the MISEP technique of nonlinear ICA. Bounded independent sources are proved to be separable through this method, apart from offset, scale and permutation indeterminacies.

We compare our results with those obtained with other approaches and with different separation models that were trained with MISEP. For the latter case we test a bilinear model and MLP-based models, using both symmetry-based regularization and the more recently proposed minimal nonlinear distortion regularization. Quantitative quality measures show that the approach that we propose is superior to the other methodologies.

Nonlinear mixing model based on the half-toning process: 2D bi-affine symmetrical mixing model (affine in each variable, and symmetrical)

where represent the mixtures and the sources.

Proof of separability of a generic nonlinear bi-affine model with nonlinear independent component analysis (nonlinear ICA):

Based on the geometric scheme of Fig.1, any bi-affine mixture of independent bounded sources is proven to be separable with the ICA criterion. The proof is based on the fact that the bi-affine transformation of each (horizontal or vertical) line of a rectangle is affine. The borders of any rectangle will thus transform in lines. Moreover, any point (X or X’) of an independent limited data (that has a rectangular support), will be transformed (mixed) as the convex combination of the corresponding horizontal and vertical line-segments, and according to the parameters of the convex combination (see Fig. 1). As a consequence of that, we conclude that, if the two points of two rectangles transform by two bi-affine transformation to the same point (T(X)=T’(X’)), then the points (X and X’) either are the same points of the same rectangle or are corresponding points of two rectangles that are simply relate by an offset and/or linear re-scale of the axis and/or rotation multiple of 90º (permutation of sources). The mixtures are thus separable apart from offset, linear scale and permutation indeterminacies.

The previous reasoning is extendable for higher dimensionally data.

This proof comprises the all the sub-models of a bi-affine mixture, namely the case bi- linear mixtures and the well know linear model.

For more details, please see the paper. (Online)

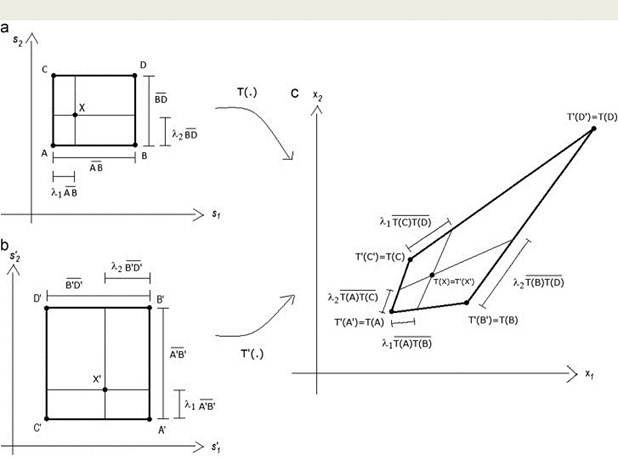
Figure 1 – The bi-affine transformation of two rectangles to the same quadrangle – geometric schem for proving the ICA separability of a bi-affine mixture.

Data:

· Tracing paper images: Results (.zip file). The mixtures can be found through the home page of Luís B. Almeida (here).

· Part of an old air mail letter: aligned and flipped data (.zip file).

· Other show-through bleed through data can be found here.

License:  This code and data are copyright of Luís B. Almeida and Mariana S. C. Almeida. Free permission is given for their use for nonprofit research purposes. Any other use is prohibited, unless a license is previously obtained. To obtain a license please contact Luís B. Almeida or Mariana S. C. Almeida. 

See, here, another method for separating linear/nonlinear show-through and bleed-through mixtures.