TwIST

     Two-step Iterative Shrinkage/Thresholding Algorithm for Linear Inverse Problems

 

 

   José Bioucas-Dias                                                    Mário Figueiredo,                                                                                               

   Instituto de Telecomunicações                                  Instituto de Telecomunicações                              

   Instituto Superior Técnico                                         Instituto Superior Técnico                                                       

   Lisboa, PORTUGAL                                               Lisboa, PORTUGAL                                             

 

Many approaches to linear inverse problems  define a solution  (e.g., a restored image) as a minimizer of  the objective function

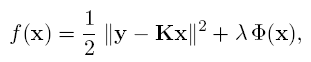
where y is the observed data, K is the (linear) direct operator,  and F(x) is a regularizer. The intuitive meaning of f is simple: minimizing it corresponds to looking for a compromise between the lack of fitness of a candidate estimate x to the observed data, which is measured by  ||y-Kx||², and its degree of undesirability, given by F(x). The so-called regularization parameter l controls the relative weight of the two terms. 

 

State-of-the-art regularizers are non-quadratic and  non-smooth; the total variation  and  the ℓp norm are two  well known examples of such regularizers with applications in many statistical inference and signal/image processing problems, namely  in deconvolution, MRI reconstruction,   wavelet-based deconvolution, Basis Pursuit, Least Absolute Shrinkage and Selection Operator (LASSO), and Compressed Sensing.

 

Iterative shrinkage/thresholding (IST) algorithms have been recently proposed to the minimization of f, with F(x) a non-quadratic, maybe non-smooth regularizers.  It happens that the convergence rate of IST algorithms depends heavily on the linear observation operator, becoming very slow when it is ill-conditioned or ill-posed. Two-step iterative shrinkage/thresholding TwIST algorithms overcome this shortcoming by implementing a nonlinear two-step (also known as "second order") iterative version of IST. The resulting algorithms exhibit a much faster convergence rate than IST  for ill conditioned and ill-posed problems. The experiments reported below illustrate the effectiveness of TwIST.

 

     MATLAB code is available here: TwIST_v2

 

     Papers describing the algorithm:

     

     J. Bioucas-Dias, M. Figueiredo, “A new TwIST: two-step iterative shrinkage/thresholding  algorithms for image restoration”,

     IEEE Transactions on Image Processing, December 2007.

 

      J. Bioucas-Dias and M. Figueiredo , "Two-step algorithms for linear inverse problems with non-quadratic regularization", 

      IEEE International Conference on Image Processing –ICIP’2007, San Antonio, TX, USA, September 2007.

 

    

 

     Experiment 1: Total-variation Phantom Reconstruction

 

     This experiment resembles the phantom reconstruction shown in [Candes et. al., 2004]:

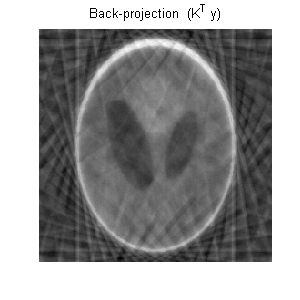
                Original data x:  256×256 Shepp-Logan phantom (Figure 1(a) )

                Linear operator K: 6136×256² matrix corresponding to  6136 locations in the 2D Fourier plane.

                                            The sampling pattern is shown in Figure 1(b)

                Observed data: y = K x

                Regularizer: Total variation

                Regularization parameter: l = 0.001

             

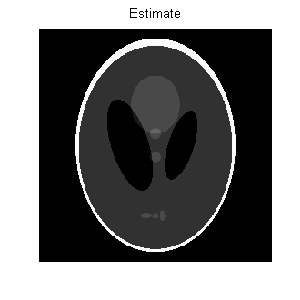
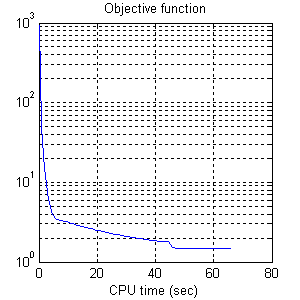
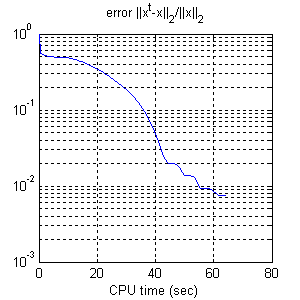
     Figure 1(d) shows the image reconstructed by TwIST. The evolution of the objective function and of the  reconstruction error

     ||x-x_orig||₂/||x_orig||₂, as a function of the elapsed CPU time, are shown in Figure 1(e) and Figure 1(f), respectively. 

    TwIST took 66 seconds in a laptop PC (with a Centrino processor running at 1.86 GHz). The final  reconstruction  error  is 8e-3.

 

Figure 1(a)	Figure 1(b)	Figure 1(c)
Figure 1(d)	Figure 1(e)	Figure 1(f)

 

Algorithm Time (sec) TwIST 66 IST 937 tveq logbarrier (l1_magic) 4827

 

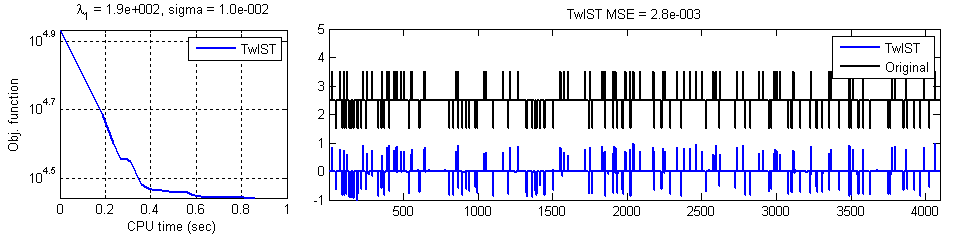
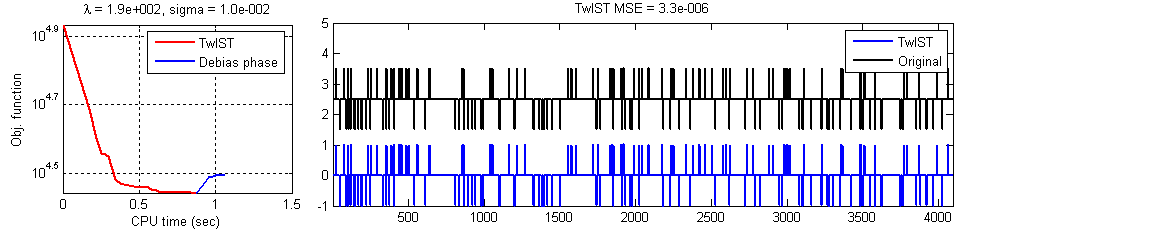
 Example 2: ℓ₁ Sparse 1D Signal Reconstruction

 

 

                Original data x:  1D signal of size 4096 only 160 of which are not zero

                Linear operator K: 1024×4096 Gaussian random matrix

                Observed data: y = K x +n (n is i.i.d. of variance s² = 1e-2)

                Regularizer:  ℓ₁  (F(x)=||x||₁)

                Regularization parameter: l = 0.1 max (||Ky^T||_¥)

 

 

The first column of Figure 2 shows the evolution of the objective as a function of the CPU time; the second column shows the original signal in black and the reconstruction in blue.  In Figure 2(a), notice that the locations of the spikes are reconstructed with high accuracy; their magnitudes are attenuated, but these can be corrected by applying a conjugate-gradient debiasing approach (as suggested here). The result of after debiasing is shown in Figure 2(b).

 

 

 

 

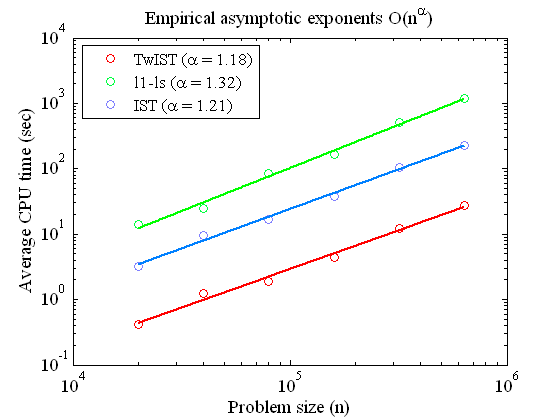
Figure 2(c) shows a comparison, in terms of computational speed, of TwIST versus IST, originally developed for wavelet-based deconvolution, described here, and the l1_ls code (March 2007), available here (from Stanford). The experimental setting is the one used before in here and here. GP The plot shows that TwIST is faster and scales more favorably (w.r.t. n, the length of the unknown signal) than the competing techniques.

Figure 2(c)

 

 

 

 Example 2: ℓ₀ Sparse 1D Signal Reconstruction

 

 

                Original data x:  1D signal of size 4096 only 100 of which are not zero

                Linear operator K: 1024×4096 Gaussian random matrix

                Observed data: y = K x +n (n is i.i.d. of variance s² = 1e-2)

                Regularizer:  ℓ₁  (F(x)=||x||₀)

                Regularization parameter: l = 20.

 

Figure 3 shows the evolution of the objective function (left) and the original and reconstructed signal (right).  Notice the quality of the reconstructed signal even without applying a debiasing step.

 

Figure 3

 

 

 

Funding Acknowledgment:

This work was partially supported by the Portuguese Fundação para a Ciência e Tecnologia (FCT),

under project POSC/EEA-CPS/61271/2004.