TwIST
Two-step Iterative Shrinkage/Thresholding Algorithm for Linear Inverse Problems
José Bioucas-Dias
Mário Figueiredo,
Instituto de
Telecomunicações
Instituto de Telecomunicações
Instituto Superior
Técnico
Instituto Superior Técnico
Lisboa,
PORTUGAL
Lisboa, PORTUGAL
Many approaches to linear inverse problems define a solution (e.g., a restored image) as a minimizer of the objective function
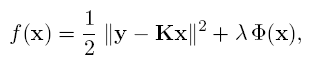
where y is the observed data, K is the (linear) direct operator, and F(x) is a regularizer. The intuitive meaning of f is simple: minimizing it corresponds to looking for a compromise between the lack of fitness of a candidate estimate x to the observed data, which is measured by ||y-Kx||2, and its degree of undesirability, given by F(x). The so-called regularization parameter l controls the relative weight of the two terms.
State-of-the-art regularizers are non-quadratic and non-smooth; the total variation and the ℓp norm are two well known examples of such regularizers with applications in many statistical inference and signal/image processing problems, namely in deconvolution, MRI reconstruction, wavelet-based deconvolution, Basis Pursuit, Least Absolute Shrinkage and Selection Operator (LASSO), and Compressed Sensing.
Iterative shrinkage/thresholding (IST) algorithms have been recently proposed to the minimization of f, with F(x) a non-quadratic, maybe non-smooth regularizers. It happens that the convergence rate of IST algorithms depends heavily on the linear observation operator, becoming very slow when it is ill-conditioned or ill-posed. Two-step iterative shrinkage/thresholding TwIST algorithms overcome this shortcoming by implementing a nonlinear two-step (also known as "second order") iterative version of IST. The resulting algorithms exhibit a much faster convergence rate than IST for ill conditioned and ill-posed problems. The experiments reported below illustrate the effectiveness of TwIST.
MATLAB code is available
here: TwIST_v2
Papers describing the algorithm:
J.
Bioucas-Dias, M. Figueiredo, “A new TwIST: two-step
iterative shrinkage/thresholding
algorithms for image restoration”,
IEEE Transactions on Image Processing, December 2007.
J. Bioucas-Dias and M. Figueiredo ,
"Two-step
algorithms for linear inverse problems with non-quadratic regularization",
IEEE International
Conference on Image Processing –ICIP’2007,
Experiment 1: Total-variation Phantom Reconstruction
This experiment resembles the phantom reconstruction shown in [Candes et. al., 2004]:
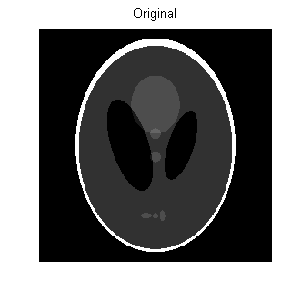
Original data x: 256×256 Shepp-Logan phantom (Figure 1(a) )
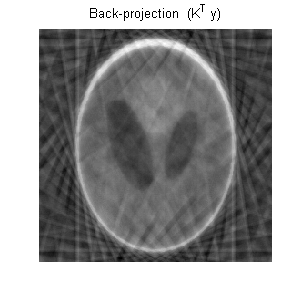
Linear operator K: 6136×2562 matrix corresponding to
6136 locations in the 2D Fourier plane.
The sampling pattern is shown in Figure 1(b)
Observed data: y = K x
Regularizer: Total variation
Regularization parameter: l = 0.001
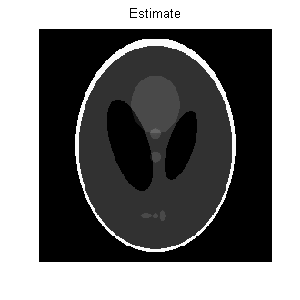
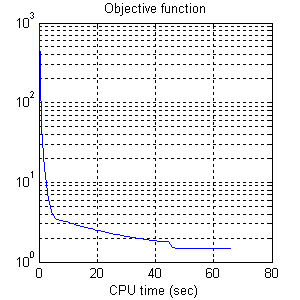
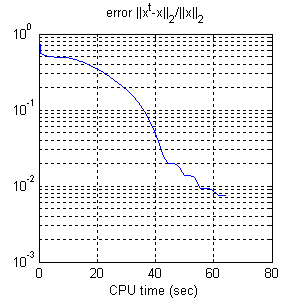
Figure 1(d) shows the image reconstructed by TwIST. The evolution of the
objective function and of the reconstruction error
||x-x_orig||2/||x_orig||2, as a function of the elapsed CPU time, are shown
in Figure 1(e) and Figure 1(f), respectively.
TwIST took 66 seconds in a laptop PC (with a Centrino processor running at 1.86 GHz). The final reconstruction error is 8e-3.
|
|
|
|
|
Figure 1(a) |
Figure 1(b) |
Figure 1(c) |
|
|
|
|
|
Figure 1(d) |
Figure 1(e) |
Figure 1(f) |
|
|
Example 2: ℓ1 Sparse 1D Signal Reconstruction
Original data x: 1D signal of size 4096 only 160 of which are not zero
Linear operator K: 1024×4096 Gaussian random matrix
Observed data: y = K x +n (n is i.i.d. of variance s2 = 1e-2)
Regularizer: ℓ1 (F(x)=||x||1)
Regularization parameter: l = 0.1 max (||KyT||¥)
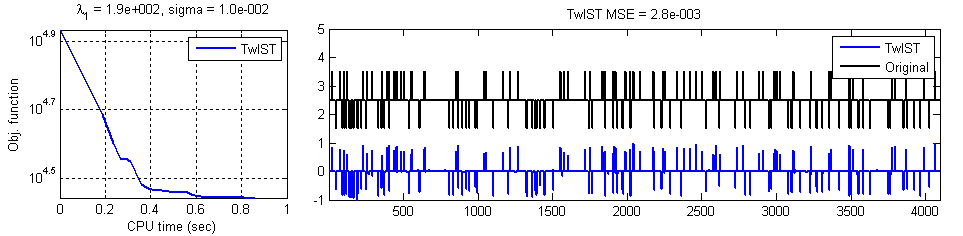
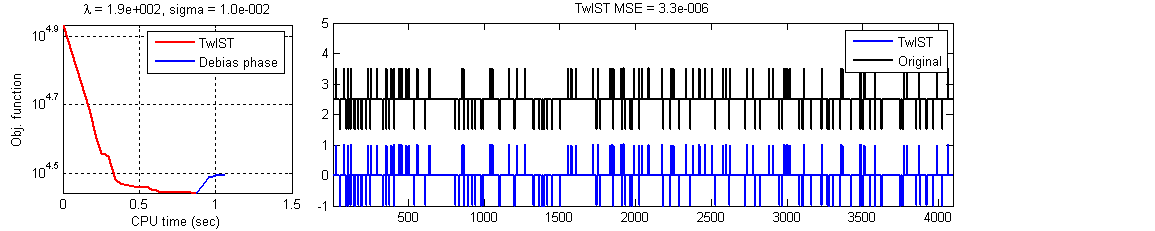
The first column of Figure 2 shows the evolution of the objective as a function of the CPU time; the second column shows the original signal in black and the reconstruction in blue. In Figure 2(a), notice that the locations of the spikes are reconstructed with high accuracy; their magnitudes are attenuated, but these can be corrected by applying a conjugate-gradient debiasing approach (as suggested here). The result of after debiasing is shown in Figure 2(b).
|
|
|
Figure 2(a) |
|
|
|
Figure 2(b) |
|
|
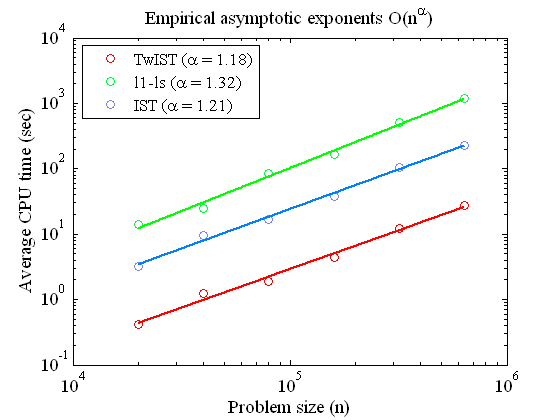
Figure 2(c) shows a comparison, in terms of
computational speed, of TwIST versus IST, originally developed for
wavelet-based deconvolution, described here, and the
l1_ls code (March 2007),
available here (from
Stanford). The experimental setting is the one used before in here and here.
GP The plot shows that TwIST is faster and scales more favorably (w.r.t. n, the
length of the unknown signal) than the competing techniques.
|
|
|
Figure 2(c) |
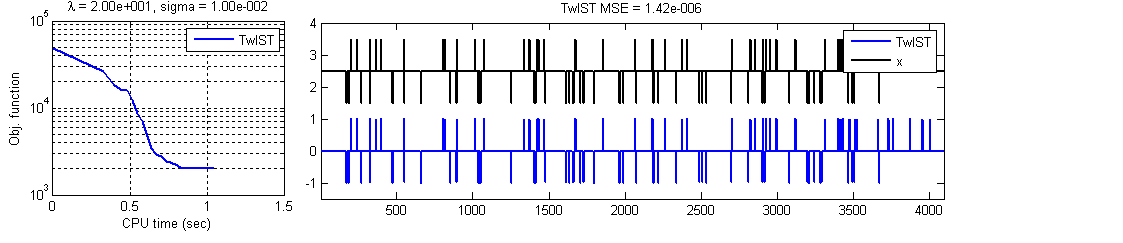
Example 2: ℓ0 Sparse 1D Signal Reconstruction
Original data x: 1D signal of size 4096 only 100 of which are not zero
Linear operator K: 1024×4096 Gaussian random matrix
Observed data: y = K x +n (n is i.i.d. of variance s2 = 1e-2)
Regularizer: ℓ1 (F(x)=||x||0)
Regularization parameter: l = 20.
Figure 3 shows the evolution of the objective function (left) and the original and reconstructed signal (right). Notice the quality of the reconstructed signal even without applying a debiasing step.
|
|
|
Figure 3 |
Funding
Acknowledgment:
This
work was partially supported by the Portuguese Fundação para a Ciência e
Tecnologia (FCT),
under project POSC/EEA-CPS/61271/2004.